TIL_2020년 9월 14일 (월)

목차

• 1.오늘 한 일
• 2.오늘 배운 것과 깨달은 것
• 3.오늘 진행한 작업물 (사진)

1.오늘 한 일

1. 컴퓨터 과학 공부
   • 부스트코스_모두를 위한 컴퓨터 과학 (CS50 2019)
   • 자료구조 (Data Structures)
     • 일정한 크기의 배열이 주어졌을 때, 그 크기를 키우려면 바로 옆에 메모리를 덧붙이는게 아니다. 실제로 다른 데이터가 있을 확률이 높기때문에, 안전하게 새로운 공간에 큰 크기의 메모리를 다시 할당하고 기본 배열의 값을 하나씩 옮겨야한다. (O(n), 배열의 크기 n만큼 실행시간이 소요될 것이다)

     • realloc 이라는 함수를 통해 수행가능.

       int *tmp = realloc(list, 4 * sizeof(int));
       

     • 데이터 구조는 우리가 컴퓨터 메모리를 더 효율적으로 관리하기 위해 새로 정의하는 구조체이다. 일종의 메모리 레이아웃, 지도라도 생각할 수 있다.
     • 배열에서는 인덱스의 값이 메모리상에 연이어 저장되어있지않다. 각 값이 메모리상의 여러 군데에 나눠져있더라도 바로 다음값의 메모리 주소만 기억하면 값을 연결해서 읽을 수 있다. 이를 ‘연결 리스트’라고 한다. 연결리스트는 각 인덱스의 메모리 주소에 자신의 값과 다음 값의 주소(포인터)를 저장한다. 마지막 값은 다음 값이 없기때문에 NULL(\0)으로 저장함.
     • node : number와 *next 두개의 필드가 함께 저장되어있음. number는 각 node가 가지는 값, *next는 다음 node를 가리키는 포인터가 됨.
     • 배열과 비교해서 연결 리스트는 새로운 값을 추가할 때 다시 메모리를 할당하지 않아도 된다는 장점이 있다
     • 연결 리스트의 크기가 n 일때 그 실행 시간은 O(n)가 된다. 배열의 경우 임의 접근이 가능하기 때문에 (정렬 되어 있는 경우) 이진 검색을 이용하면 O(log n)의 실행 시간이 소요 되는 것에 비해서 다소 불리하다. 여러 데이터 구조는 각각 장단점이 존재한다. 목적에 부합하는 가장 효율적인 데이터 구조를 고민해서 사용해야한다.
     • 트리 : 연결리스트를 기반으로 하는 새로운 데이터 구조.
     • 연결리스트는 1차원적으로 구성되어있다면, 트리에서의 노드들은 2차원적으로 연결되어있다. 각 노드는 일정한 층에 속하고, 다음 층의 노드들을 가리키는 포인터를 가지게 된다.
     • 가장 높은 층에서 트리가 시작되는 노드를 ‘루트’라고 하고, 다음 층의 노드들을 ‘자식 로드’라고 한다.
     • ‘이진 검색 트리’ 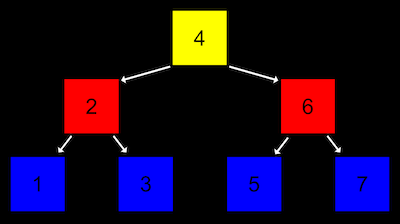왼쪽자식노드는 자신보다 값이 작고, 오른쪽자식노드는 자신보다 값이 큽니다. 이는 이진 검색을 수행하는데 유리함
     • 해시테이블은 연결리스트의 배열. 각 값들은 해시 함수를 통해 어떤 바구니(ex. 이름 바구니)에 담길지 결정됨. 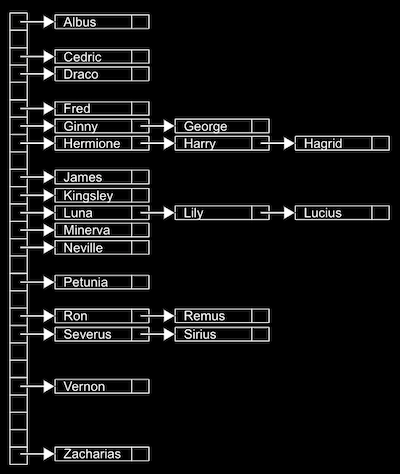검색시간은 O(1)가 된다. 왜냐하면 이름의 길이는 더 늘어날 수 없는 상수(const)이기 때문이다.
     • 트라이는 트리형태의 자료구조. 각 노드가 배열로 이뤄져있는 것이 특징이다. 이름 주소록을 생각해보면 쉽다. A ~ Z 까지 26개의 인덱스를 만들고 AA, AB 등의 인덱스를 또 만들고 AAA, AAB 의 인덱스를 만들고 이렇게 간다. 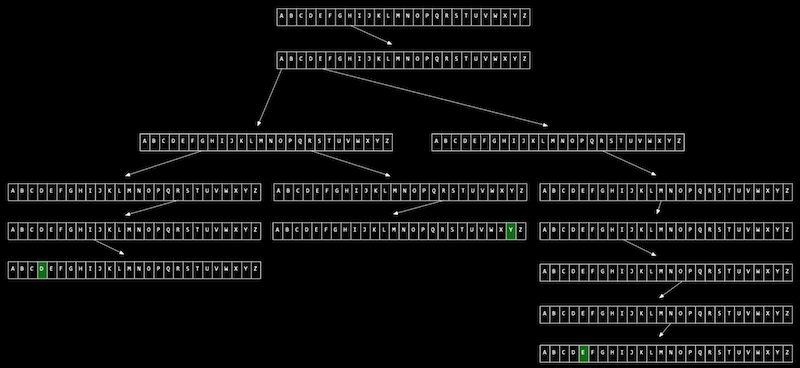트라이에서 값을 검색하는데 걸리는 시간은 ‘문자열의 길이’에 의해 한정됨.
     • 검색속도가 매우 빠른 장점이 있지만 그만큼 많은 메모리를 사용하는 단점이 있다.
     • 큐 : 메모리 구조에서 값이 아래로 쌓이는 구조. 선입선출(FIFO)의 방식. - 배열이나 연결리스트를 통해 구현
     • 스택 : 값이 위로 쌓이는 구조. 후입선출(LIFO)의 방식. 배열이나 연결리스트를 통해 구현.
     • 딕셔너리 : 키와 값이라는 요소로 구성되어있음. 키에 해당하는 값을 저장하고 읽는 것. 어떻게 키를 정의할 것인지 매우 중요함.

2.오늘 배운 것과 깨달은 것

• 드디어 CS50 수업 끝! 재미있었다. 하버드는 학생뿐만 아니라 교수님도 수업방식도 참 뛰어나구나… 내일부터는 다른 것을 공부하자!

3.지금까지 작업물 (사진)

• 없음.